図形の証明問題3題出題します。
そのうちの2つについては、解き方が複数ある問題を作ってみました。解き方が1つではないので、どの箇所とどの箇所が等しいのか、どの角とどの角が等しいのか、というのを見る能力を養ってください。
問題
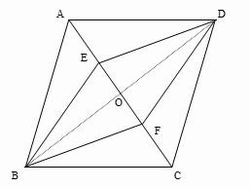
平行四辺形ABCDに対角線を引き、交点をOとする。
対角線AC上に、OE=OFとなるように、点Eと点Fをとる。
(1) 四角形DEBFが平行四辺形であることを証明しなさい。
⇒解答例はこちら(jpg画像)
メモ
難易度:
問題集などでよく見られます。基本的な問題なので、覚えてしまいましょう。
(2) △ADE≡△CBFを証明しなさい。
⇒解答例はこちら(jpg画像)
メモ
難易度:
解き方は1つだけではありません。(1)の条件を利用してもよいです。複数の解き方を考えてみましょう。
問題
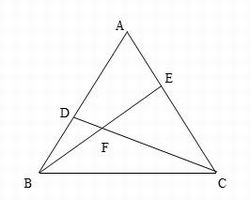
正三角形ABCに、AE=BDとなるように、点Dと点Eをとる。
線分BEと線分CDの交点をFとしたとき、△ABE∽△FBDを証明しなさい。
なお、点D、点Eはそれぞれ、点B、点C上にはないものとする。
⇒解答例はこちら(jpg画像)
メモ
難易度:
気が付けば、とても簡単なのですが、気が付かなければ、難しいかも。いきなり相似条件を並べて解かないこと、がポイントです。
問題
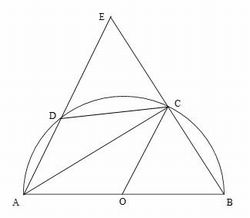
点Oを中心とする半円Oがある。線分ABは直径であり、弧AB上に∠ABCが45度を超えるように点Cをとり、点Oと結ぶ。弧AC上に弧BC=弧CDとなるように点Dをとり、点Cと結ぶ。直線BCと直線ADとの交点をEとする。
(1) △ABC≡△AECを証明しなさい。
⇒解答例はこちら(jpg画像)
メモ
難易度:
円周角の定理を使った、基本的な問題です。
(2) (1)から求められる条件を使用して、△OBC∽△CEDを証明しなさい。
⇒解答例はこちら(jpg画像)
メモ
難易度:
これも解き方は1つだけではありません。複数の解き方を考えてみてください。
今年で11年目の「駿英ネットサービス」で無駄のない受験勉強を!
●県立入試ラストスパート問題
●受験校のメール相談
力になります!「駿英ネットサービス」をご検討下さい^^
入試過去問のオンライン解説・添削コースやっています。
【3学期生徒募集】自分に合った勉強方法を見つけよう!
今学年の成績がパッとしない生徒は学習環境の見直しが急務!ズルズルと時間が経過しないよう今の勉強方法で良いのか自問自答してみよう!
駿英の指導は
●中学生コースは5教科指導可能
●徹底した新教研テスト対策
●映像授業とは全然違う高校生への直接指導
●どのレベルも分かりやすいと評判の高校数学
●スペシャリスト揃いの高校コース
駿英の個別指導は完全完全1対1!家庭教師そのままの授業を教室にて行います^^
ぜひ、駿英の家庭教師&教室指導をご検討ください^^
※映像授業で高校数学が分からない時はお早めに!スペシャリストが待っています^^
※難関大学用数学・物理、私大用古文など指導できる先生は限られてきます。まずはお問合せ下さい。



コメント一覧
コメントする