【コスパ学習】関数のグラフで4点ゲット(中級編)

　今日（2月13日）の新聞に、前期選抜の出願先変更状況が載っていましたね。
一般出願で大きく変動があったのは、橘が14名減の307名、福島西が10名減の236名、郡山の普通科が16名減で248名でした。

　出願先の変更は、15日までなので、まだ変更が予想されますが、受験生にとっては、ライバルが１人でも少ないほうがいいですよね。

　出願者数が増えたらどうしよう…といったことに限らず、受験が近づくにつれて、いろいろな不安が起きるかもしれませんが、そのときは、いったんそのことから目を背けて、問題を解くなどして、勉強に意識を集中することをお勧めします。別のことに集中しているときは、不安になる余裕がないですからね。

　それでは、コスパ学習の続きに入りましょう。

前回は簡単な直線のグラフでしたが、今回はもう少し直線を増やしてみましょう。

問題は2問です。面積や座標を考える問題ですが、問題３と４とでは、解き方が異なります。問題4では、相似な図形を利用して解いてみてください。

なぜ2通りの解き方をさせるかというと、問題の内容によっては、座標を利用するよりも、図形の相似比などを使って解いたほうが、はるかに楽なことが多いからです。

例えば、今回の新教研テスト2月号、大問６の（３）は、4本の直線の式をわざわざ求めなくとも、平行線と線分の比の考え方などを使えば、楽に求めることができますよ。

それでは問題です。それぞれの制限時間は10分です。

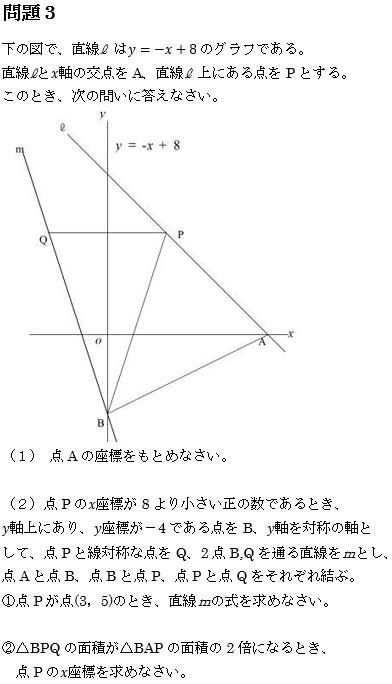
難易度は、
（１）1
（２）①2
（２）②3.5
といったところですね。

問題３の解答はこちら。
（１）と（２）①

（２）②

難易度は
（１）1
（２）①2
（２）②4.5
かな。最後の問題は時間がかかるかもしれませんね。

問題４の解答はこちらです。
（１）と（２）①

（２）②

問題３、問題４ともに最初の２問は難易度が低く、練習すれば必ず解けるコスパが高い問題なので、確実に解けるように練習しましょう！

次回は、放物線のグラフを取り上げる予定です。

■ 雑記 ■

問題を作成するとき、一応３問までとしているのですが、作りすぎたりもします。
今回出題した問題４は、最初５問でした。

本当は、最後の問題を「△AOEの面積をｔを使って表す」としたかったのですが、そうすると制限時間の１０分では解けないと思い、割愛しました。

この問題の解き方は数種類ありますが、問題４（２）②の解答を参考にすれば、楽に解けるはずです。

気になる方は、ぜひチャレンジしてみてください。

解答は、次回お知らせします。

by　金田