本日、入試前最後の日曜日でした。
私も朝から受験生にラストスパートを行ってきました。
直前指導ですので教科は理、社、数が中心でした。
理社は塾用問題集と教科書を使いながら確認&練習。
数学は入試や模試の過去問&自作問題で実戦練習。
数学は福島入試にぴったりの問題集がなく、皆さんも苦労していると思います。
以前アップした「連立応用問題」や「図形の証明問題」の記事へのアクセスが多いのもその表れかと・・・
そこで今回は生徒に使っている数学の「直前仕上げ問題」をシェアします。良かったら使ってください^^
今回は予定外のアップ。記事は特にありません。
あ、「5点アップ作戦シリーズ」が好評のようで良かったです。明日、「直前5点アップ~ラスト」記事をアップしますね。
令和4年 入試直前用「数学」仕上げ問題8!
私が週末に使用した「数学」問題の一部をシェアします。
福島県の入試「数学」でカギを握る
●連立方程式2題
●図形の証明問題2題
●関数の応用問題2題
●空間図形の応用問題2題
になります。
なお、解答は一番下に付けますが解説はありませんのでご了承下さい。分からない問題の解説は学校や塾の先生に頼って下さい^^;
あ、駿英の塾生やネットサービス会員は解説が欲しいときはメール下さい。メールにて解説します。塾生は下のフォームから「解説が欲しい問題」「名前」を添えて送信下さい。
「メッセージ」フォームはこちらです
『方程式の利用』~仕上げの2題
こちらはオリジナル問題。どちらも正解率は高めです。
問題1
あるコーヒー店では、100gずつ袋に入れてコーヒー豆を売っており、コーヒー豆Aは100gで700円、コーヒー豆Bは100gで600円、コーヒー豆Cは100gで500円である。明君は毎月4袋(400g)ずつ、この店でコーヒー豆を買う。1月から6月までの6ヶ月間にコーヒー豆Bは800g買っており、支払った代金の合計は14800円であった。
この6ヶ月間に買ったコーヒー豆Aとコーヒー豆Cはそれぞれ何gか。求める過程も書きなさい。
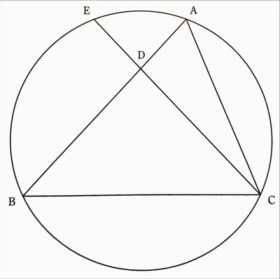
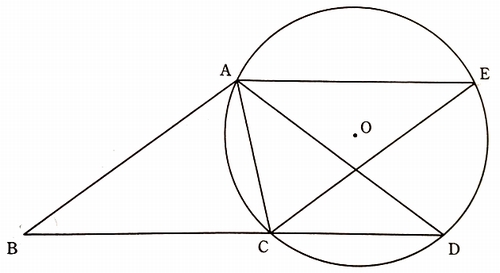
『図形の証明』~仕上げの2題
円が入った証明問題を練習しておこうと直前練習しました。
こちらは福島県の過去問です。
『関数の応用問題』~仕上げの2題
関数の応用問題です。今年は「二次関数と一次関数の融合」だと思いその練習をしています。
こちらはオリジナル問題と模試過去問になります。
問題6
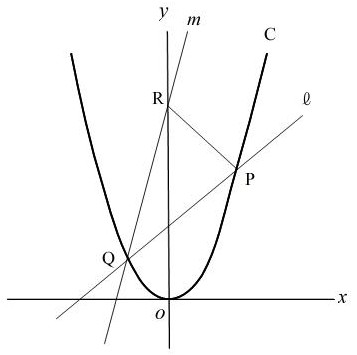
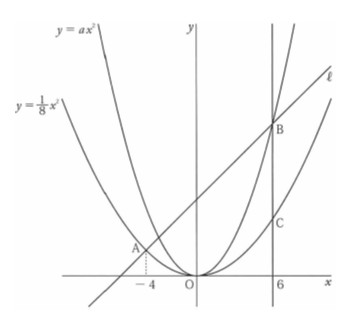
下の図のように、 関数\(y=ax^2\)のグラフと関数\(y= \frac{1}{8}x^2\)のグラフがある。関数\(y= \frac{1}{8}x^2\)のグラフ上にx座標が-4である点Aをとり、 関数\(y=ax^2\)のグラフ上にx座標が6である点Bをとる。
2点A、 Bを通る直線をℓとすると、ℓの式はy=x+6である。また、Bを通り、y軸に平行な直線と関数\(y= \frac{1}{8}x^2\)のグラフとの交点をCとする。
このとき、次の(1)~(3)の問いに答えなさい。
(1) aの値を求めなさい。
(2) △AOCの面積を求めなさい。
(3) y軸上に△AOBの面積と△DOBの面積が等しくなる点Dをとる。
また、線分AD、DB上を動く点P、線分AO、OC上を動く点Qを、線分PQがy軸と平行となるようにとる。
PQ=8となるPのx座標をすべて求めなさい。ただし、Dのy座標は正とする。
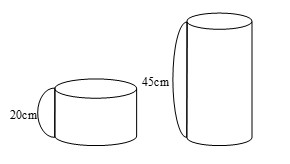
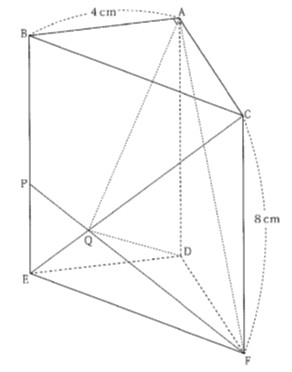
『空間図形の応用問題』~仕上げの2題
今年は三角柱、四角柱の問題だと予想しその練習をしています。
こちらは生徒から質問の多かった模試の過去問になります。
■ 雑記 ■
昨日今日と働き過ぎでヘロヘロです。
今夜は仕事を終えたのでこれから赤霧島でもお湯割りしながら洋ドラ見ます。
ハマっているのが「ブラックリスト」!メチャ面白いです♪
by 渡部
受験勉強といっても「何をやったら良いの?」と分からないもの。
駿英では福島県立入試に最適化した学習内容、勉強方法を『駿英ネットサービス』で提供してきました。昨年も多くの受講生が志望校合格を果たしています。13年目を迎え更にパワーアップ!

まずは6月から始まる
●実力テスト
●新教研テスト
の対策を『駿英ネットサービス』で始めよう!6月中はお得なキャンペーン付です!!
駿英のこだわりはマンツーマン指導とスペシャリストの講師陣。言葉より実績を見て下さい!
2025年の駿英は
●教室(郡山市桑野)での個別指導
●家庭教師
●オンライン家庭教師
の指導形態。
生徒1人1人に応じた指導を経験豊富な講師陣が行います。指導教科もテキストも生徒の要望に応じプラン作成。だからひと味違います。まずは体験学習で違いを実感下さい。

【高校生コース】
駿英は生徒の学力に応じた指導をするから成績に直結!小さな塾なのに今年も東北大、県立医大医学部、看護学部、保健学部、東京海洋大、明治大4名、法政大、東洋大、東京理科大、新潟県立大、会津大、千葉工大に合格!生徒に合せた受験対策をするから入試にめちゃ強いんです^^ 先生は英数指導可。物理・化学・古文・小論文など専門の先生も待機中です。
【中学生コース】
駿英の先生は1対1指導で5教科対応!生徒1人1人に応じた指導をしますので定期試験はもちろん新教研対策も生徒に合せて対策 します。とにかく高校受験に強いのが駿英の特長です!渡部、金田、鈴木も待機中!
「質問&相談」フォーム
お問い合わせ(LINE公式)
フリーダイヤル 0120-593-645










コメント一覧
コメントする